TRUE AND FALSE TYPE QUESTIONS 1 When 14x 3 – 3x 2 4x 2 is divided by 2x – 1, the remainder is 5 2 4x 2 – 8x 15 is exactly divisible by 2x – 1 3 x 2 – 5x 6 cannot be written as a product of two linear factors 4 x 3 – 3x 2 y 3xy 2 – y 3 is exactly divisible by x – y 5 (2a b) 2 – (2b a) 2 = 3(a 2 – b 2) is an identify 6 (x 2 1) 4 = (x 4 – 6x 2 1The perfect cube forms (x y) 3 (xy)^3 (x y) 3 and (x − y) 3 ( xy)^3 (x − y) 3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often Definition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly, doing

Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 6 Access Free Pdf
Expand (1/x+y/3)^3 class 9
Expand (1/x+y/3)^3 class 9-To find the tenth term, I plug x, 3, and 12 into the Binomial Theorem, using the number 10 – 1 = 9 as my counter 12C9 ( x) 12–9 (3) 9 = (2) x3 (196) = x3 Find the middle term in the expansion of (4x – y)8 Since this binomial is to the power 8, there will be nine terms in the expansion, which makes the fifth term the middle oneClass XICBSEMathematics Polynomials Practice more on Polynomials Page 2 wwwembibecom Hence the given expression x 10 y 3 t 50 is not a polynomial in one



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community
R S Aggarwal and V Aggarwal Solutions for Class 9 Mathematics CBSE, 3 Factorisation of Polynomials All the solutions of Factorisation of Polynomials Mathematics explained in detail by experts to help students prepare for their CBSE examsDesmos offers bestinclass calculators, digital math activities, and curriculum to help every student love math and love learning math Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10
If ` (x)/(y)(y)/(x)=1`, where` x,y ne 0` then the value of `(x^3y^3)` is A 1 B 1 C 0 D `(1)/(2)` class9; Ex 32, 11 If x 8(2@3) y 8(−1@1) = 8(10@5) , find values of x and y x 8(2@3) y 8(−1@1) = 8(10@5) 8(2𝑥@3𝑥) 8(−𝑦@𝑦An adfree subscription with Shaalaacom provides you an adfree experience across our site and app for your account The benefits of an adfree subscription will allow you to focus on what's important and also speeding up the experience by removing
They have the same value for all values of \ (xExample Expand 3 × (52) Answer It is now expanded We can also complete the calculation 3 × (52) = 3 × 5 3 × 2 = 15 6 = 21 In Algebra In Algebra putting two things next to each other usually means to multiply So 3(ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbersIn mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremCommonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written () It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 x) n, and is given by the formula =!!()!For example, the fourth power of 1 x is




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Please Expand 1 X Y 3 Whole Cube Brainly In
Transcript Ex 25, 6 Write the following cubes in expanded form (i) (2x 1)3 (2x 1)3 Using (a b)3 = a3 b3 3ab(a b) Where a = 2x & b =1 = (2x)3 (1)3 3(2x)(1) (2x 1) = 8x3 1 6x(2x 1) = 8x3 1 12x2 6x = 8x3 12x2 6x 1 Ex 25, 6 Write the following cubes in expanded form (ii) (2a 3b)3 (2a 3b)3 Using (x y)3 = x3 y3 3xy(x y) Where x = 2a & y = 3b = (2a)3Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams This chapter mainly deals with problems based on expansions Experts tutors have formulated the solutions in a step by step manner for students to grasp the concepts easily From the exam point of view, solving




Binomial Theorem Solutions Examples Videos




Expand 1 X Y 3 3 Solve It Fastly Brainly In
Worked examples 1 5y 15 = 5 × y 5 × 3 (HCF is 5) 2 21 x − 24 y = 3 × 7 x − 3 × 8 y (HCF is 3) = 5(y 3) = 3(7 x − 8 y) 3 12 ab 18 a = 6 a × b 6 aClick here👆to get an answer to your question ️ If x y = 12 and xy = 27 , find the value of x^3 y^3 eg {1, 2, 3, 6, 9, 18} is the set of factors of 18 expand factorise 5a(a − 2) 5a2 − 10a 'Gnidnapxe' is the reverse of 'expanding' It's 'factorising', you dummy!




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Write expression log(x4y7 z16) log ( x 4 y 7 z 16) as a sum or difference of logarithms with no exponents Simplify your answer completely log(x4y7 z16) = log ( x 4 y 7 z 16) = Get help Box 1 Enter your answer as an expression Example 3x^21, x/5, (ab)/c Be sure your variables match those in the questionWe can skip n=0 and 1, so next is the third row of pascal's triangle 1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so not(),where f (n) (a) denotes the n th derivative of f evaluated at the point a
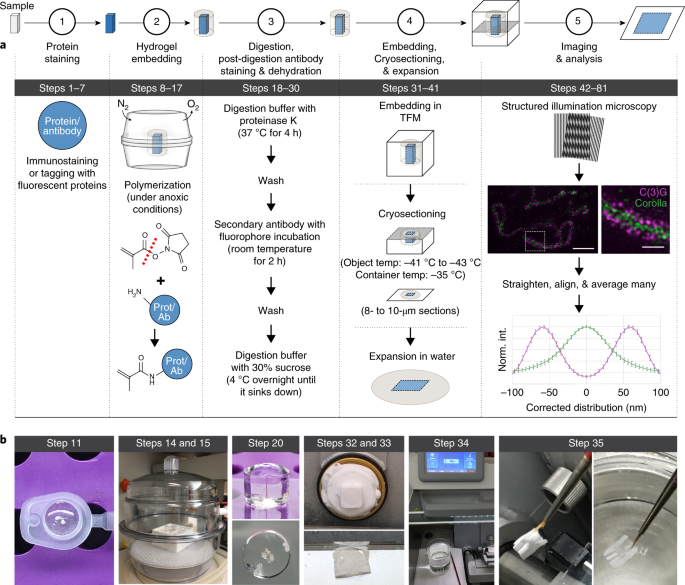



Combined Expansion Microscopy With Structured Illumination Microscopy For Analyzing Protein Complexes Nature Protocols




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
Suppose we want to expand (2xy)3 We pick the coefficients in the expansion from the relevant row of Pascal's triangle (1,3,3,1) As we move through the terms in the expansion from left to right we remember to decrease the power of 2x and increase the power of y So, (2xy)3 = 1(2x)3 3(2x)2y 3(2x)1y2 1y3 = 8x3 12x 2y 6xy y3 ExampleFactorisation is the opposite process of expanding brackets For example, expanding brackets would require \ (2 (x 1)\) to be written as \ (2x 2\) Factorisation would be to start with \ (2x 2\) and end up with \ (2 (x 1)\) The two expressions \ (2 (x 1)\) and \ (2x2\) are equivalent;Find (3 x) 3 The power that we are expanding the bracket to is 3, so we look at the third line of Pascal's triangle, which is 1 3 3 1 So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally



Ambiguous Pemdas




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education
2x 3y = 5 3y = 5 2x Table of solutions X –1 2 y –1 –3 We plot the points (–1, –1) and (1, –3) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 2x 3y = –5 x y = –1 ⇒ y = – 1 – x Table of solutions X 0 1 y –1 –2 We plot the points (0, –1) and (1, –2) on the same graph paper and join the same by a ruler toDefinition The Taylor series of a real or complexvalued function f (x) that is infinitely differentiable at a real or complex number a is the power series ′ ()!() ″ ()!() ‴ ()!() ,where n!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



What Is The Answer Of X Y Quora



How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic
Brainlycom For students By students Brainly is the place to learn The world's largest social learning network for students👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms or5 Classify the following as linear, quadratic and cubic polynomials ∵ The degree of x 2 x is 2 ∴ It is a quadratic polynomial ∵ The degree of x – x 3 is 3 ∴ It is a cubic polynomial ∵ The degree of y y 2 4 is 2 ∴ It is a quadratic polynomial ∵ The degree of 1 x is 1




Ncert Solutions For Class 11 Maths Chapter 8 Binomial Theorem Ex 8 2 Zoefact




1 X Y 3 3 Expand Brainly In
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables Exercise 43 1 Draw the graph of each of the following linear equations in two variables (i) xy = 4 Solution To draw a graph of linear equations in two variables, let us find out the points to plot2x315=1515 becomes 2x18=0 You are moving the 15 to the left side of the equals So, the right side becomes 0 This does not help you solve the equation it just gives you extra work steps You should always focus on the location of the variable (the left side in this equation) and move numbers away from that sidePhone support is available MondayFriday, 900AM1000PM ET You may speak with a member of our customer support team by calling End of Conversation Have a great day!




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium
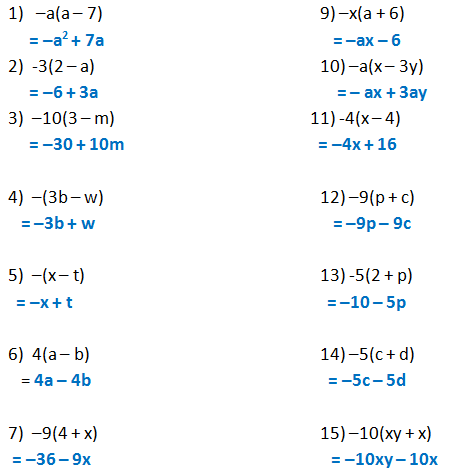



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
Class 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, grouping, AC method), completing the square, graphing and othersSolution (i) The example of monomial of degree 1 is 5y or 10x (ii) The example of binomial of degree is 6x x 11 or x 1 (iii) The example of trinomial of degree 2 is x 2 – 5x 4 or 2x 2 x1 Question 7 Find the value of the polynomial 3x 3 – 4x 2 7x – 5, when x = 3 and also when x = 3



Arxiv Org Pdf 16 3990




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf
= x 3 1 x 2 x = (iv) (x − y) 3 Solution Using formula, (x – y) 3 = x 3 – y 3 – 3xy(x – y) (x − y) 3 = x 3 − y 3 – 3(x) yx − y = x 3 – y 3 – 2x 2 y xy 2 Question 7 Evaluate the following using suitable identities (i) (99) 3 Solution 99 = 100 – 1First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More ExamplesAfter having gone through the stuff given above, we hope that the students would have understood "How to Find Coefficient of x in Binomial Expansion"Apart from the stuff given above, if you want to know more about "How to Find Coefficient of x in Binomial Expansion" Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here



1
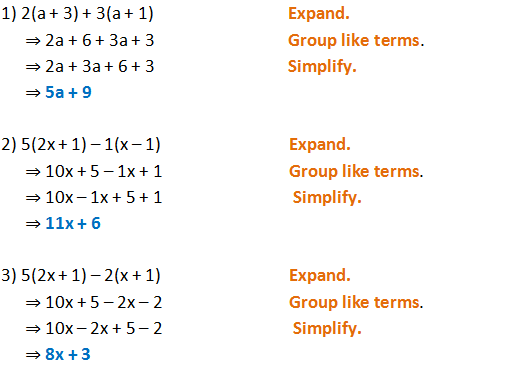



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)nPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2Selina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 5 Factorisation All the solutions of Factorisation Mathematics explained in detail by experts to help students prepare for their ICSE exams



How To Solve For X And Y In X Y 5 And Xy 6 Quora




How To Use The Binomial Theorem In 1 X 1 2 Quora
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions, combining several fractions into one andFree graphing calculator instantly graphs your math problems
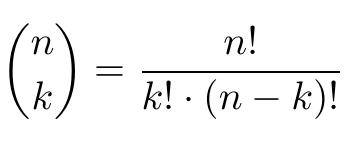



Binomial Coefficient Calculator




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 6 Access Free Pdf
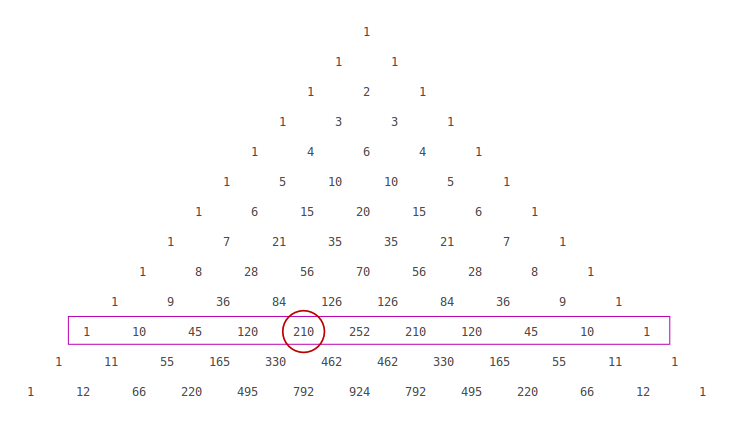
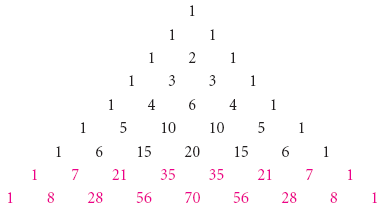
INFINITE SERIES 415 n 1 5 10 2 3 n We observe that as n becomes larger and larger, 2 3 n becomes closer and closer to zeroSteps for Solving Linear Equation 3x4y=3 3 x − 4 y = 3 Add 4y to both sides Add 4 y to both sides 3x=34y 3 x = 3 4 y The equation is in standard form The equation is in standard formTo generate Pascal's Triangle, we start by writing a 1 In the row below, row 2, we write two 1's In the 3 rd row, flank the ends of the rows with 1's, and add latex11/latex to find the middle number, 2 In the latexn\text{th}/latex row, flank the ends of the row with 1's



Ambiguous Pemdas




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials
Share It On Facebook Twitter Email 1 Answer 0 votes answered by Atthar (434k points) selected by Maniraj Best answer Correct Answer CDenotes the factorial of nIn the more compact sigma notation, this can be written as = ()! 862 views around the world You can reuse this answer Creative Commons License




Conic Section From Expanded Equation Ellipse Video Khan Academy




Find The 7th Term In The Expansion Of 4x5 52x 8



Www Math Ucla Edu Mt 131a 1 02s 131a Hw Sol Pdf
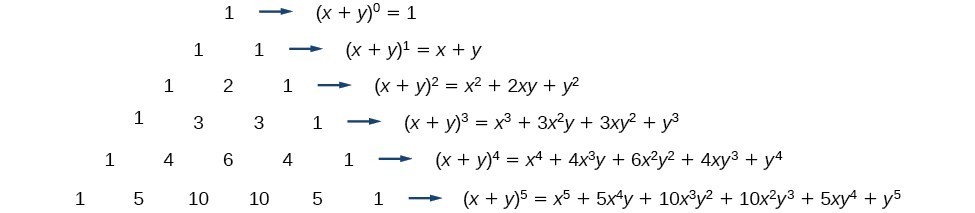



Use The Binomial Theorem College Algebra



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks



Obtain The Binomial Expansion For 1 2x 5 Use Your Expansion To Evaluate 0 98 5 To Five Tutorke




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf
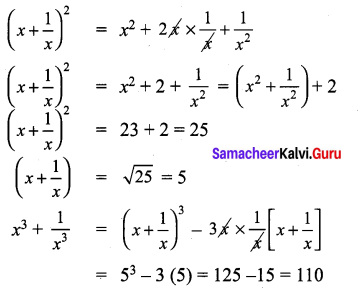



Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3 4 Samacheer Kalvi



Http Www Stat Wisc Edu Ifischer Calculus Pdf
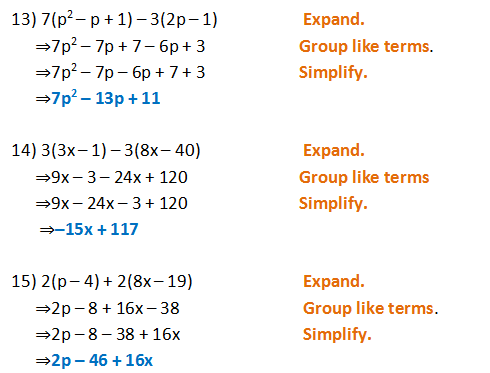



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths




Binomial Theorem Wikipedia




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube



Www Shorelineschools Org Cms Lib Wa Centricity Domain 18 Math 5 11 copy Pagenumber Pdf




Expand 1x Y3 3 Maths Questions




Machine Learning Stanford Coursera Week 1 Quiz 2 For The Github Repo Github Com Mgalarnyk Datasciencecoursera Tree Master Stanford Machine Learning Github




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




How To Evaluate Determinants Without Expanding




Algebra Formulas For Class 9 Pdf Download Free Here




The Solution Of The Differential Equation 1 Y X 2y Dx X




Algebraic Identities Of Polynomials A Plus Topper




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Expand 1 X Y 3 3 Novocom Top



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation
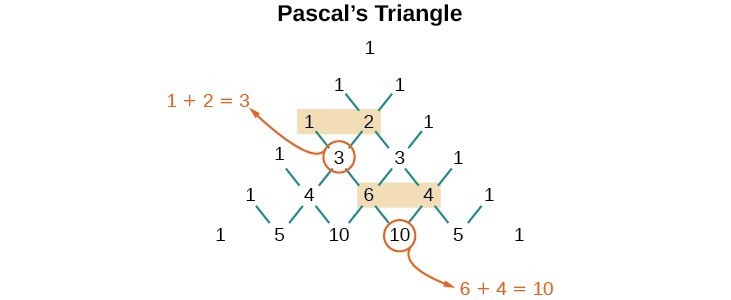



Use The Binomial Theorem College Algebra




Taylor Mclaurin Series Questions And Answers Sanfoundry



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9




Expand X X Y 3 3xy X Y




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
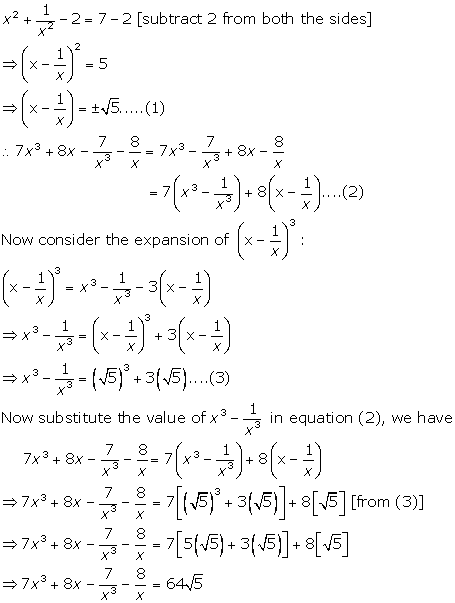



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Factorisation Algebraic Expressions Siyavula
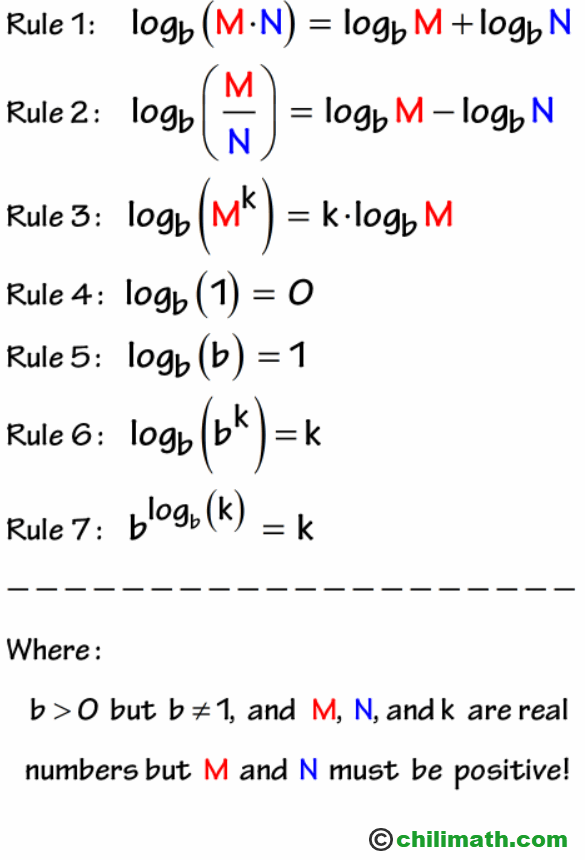



Expanding Logarithms Chilimath




Taylor Series Wikipedia



1



Www Shorelineschools Org Cms Lib Wa Centricity Domain 18 Math 5 11 copy Pagenumber Pdf




Expand 1 X Y 3 3 Novocom Top




Selina Concise Mathematics Class 9 Icse Solutions For Chapter 3 Expansions




Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Use The Binomial Theorem College Algebra




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities
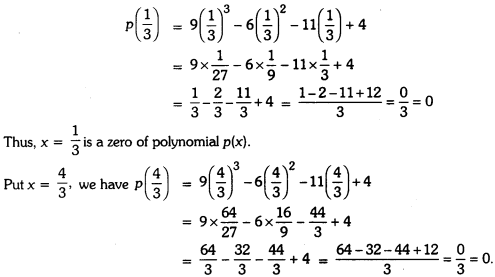



Polynomials Class 9 Extra Questions Maths Chapter 2 With Solutions Answers
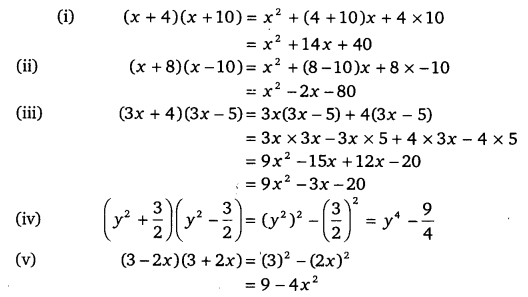



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Please Expand 1 X Y 3 Whole Cube Brainly In



Q Tbn And9gcqw3ytr8shmxjcu2 37v8gqgdbytzhzbbgxwcuepfumanvsy3e4 Usqp Cau




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions
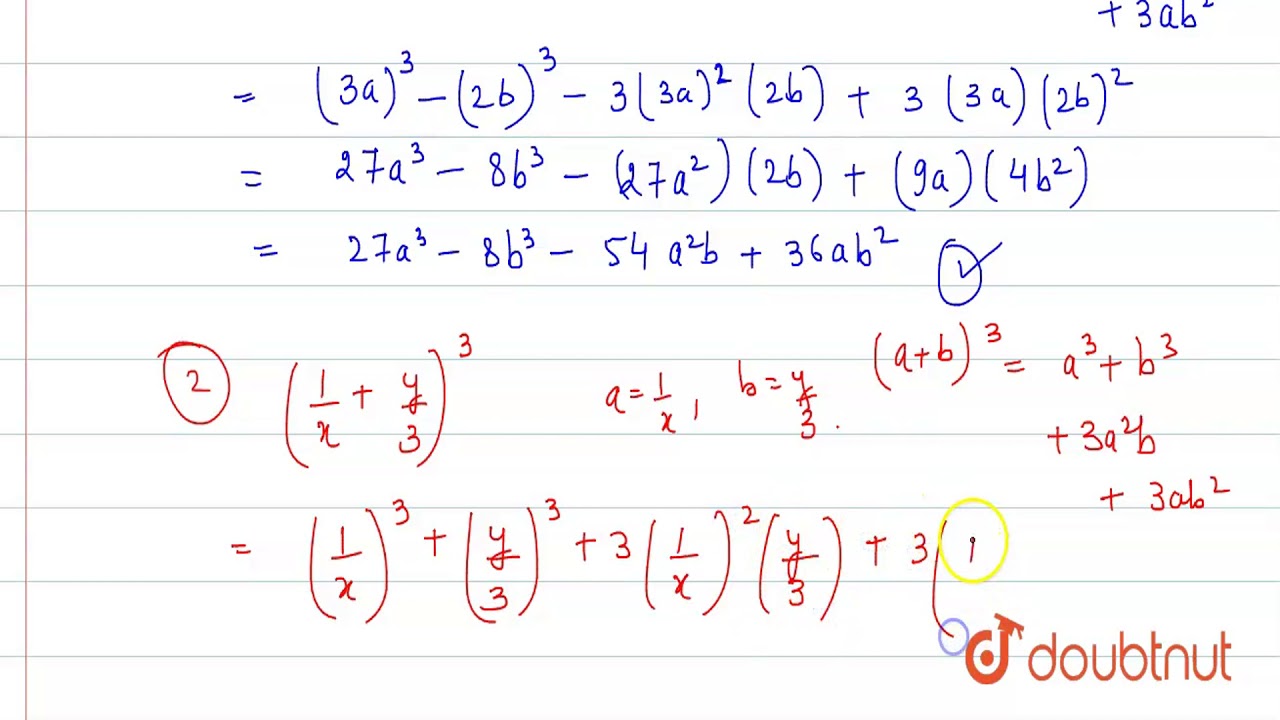



Expand The Following I 3a 2b 3 Ii 1 X Y 3 3 Iii 4 1 3x 2 Youtube



Mrurbanc Weebly Com Uploads 4 4 2 6 Pages From Hl Exam Review Assignment Answers Part 1 Pages 01 Pdf




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



Kumarsir34 Files Wordpress Com 21 02 Maths Class X Sample Test Paper 08 For Board Exam 21 Answers Pdf



Http 300math Weebly Com Uploads 5 2 5 1 Eqao Prep Pdf




Expanding Algebraic Expressions Chapter Algebraic Expressions Siyavula
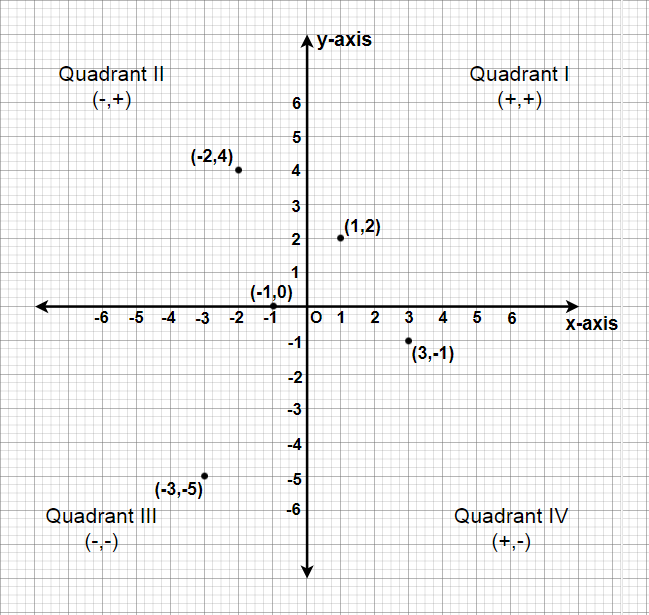



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks




Taylor Series Wikipedia




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions



Expand 1 X Y 3 Whole Cube Studyrankersonline




Expanding Binomials Video Polynomials Khan Academy




Omtex Classes X Y 3 And X Y 4 Complete The Following Table To Draw Graph Of The Equation
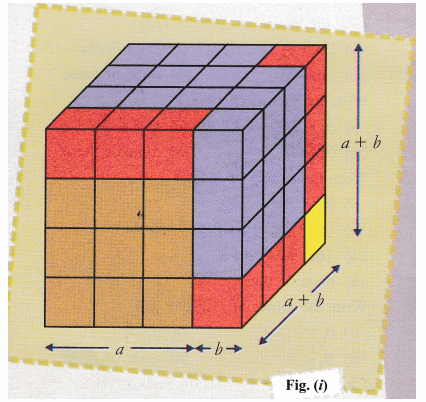



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2



How Do I Use The Binomial Theorem To Find The Constant Term Socratic




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



Cbse 9 Math Cbse Polynomials Ncert Solutions



Factorials To Binomial Theorem




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download




Find Middle Term For Even Power Binimial Expansion Youtube



4 The Binomial Theorem




Expand 1 3 X 2 3 Y Whole Cube Brainly In




Binomial Theorem Concept And Applications Handa Ka Funda Online Coaching For Cat And Banking Exams



Q Tbn And9gctrpod5wp0yfbr8op Svklbrvw6frcvhr0kqyrjgtgvhuqyyxiu Usqp Cau




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities



Evaluate 104 Cube Using A Suitable Identity Studyrankersonline




Pc 9 5 Ppt 9 5 The Binomial Theorem Let U19s Look At The Expansion Of X Y N X Y 0 1 X Y 1 X Y X Y 2 X2 2xy Y2 X Y 3 X3 3x2y 3xy2 Y3 X Y 4 X4 Course Hero



0 件のコメント:
コメントを投稿